ELECTRONIQUE 3D
L'ELECTRONIQUE FACILE ET AMUSANTE

Charge et décharge d'un condensateur 
dans une résistance 

- Énergie emmagasiné par le condensateur : 

- Pour commencer il faut savoir à quoi correspond le farad (C). Celui-ci correspond à une charge emmagasiné de 1 Coulomb sous un potentiel de 1 Volt (U). 
 
Q = C*U avec U= différence de potentiel à ses bornes, C (Farad). Le farad étant très grand, on utilise les sous multiples : 
Millifarad 10-3 F, Microfarad 10-6 F, Nanofarad 10-9 F, Picofarad 10-12 F 
 
De cette formule en découlent deux autres. C=Q/U et U=Q/C 
 
- L'énergie (W) exprimée en joules, se calcule par la relation W = 0,5 C*U2 avec C= capacité en farads et U= différence de potentiel aux bornes du condensateur.en volts. Par exemple si l'on prend des valeurs rondes, un condensateur de 1000 µF chargé sous une tension de 100V. W = 5 joules. 
 
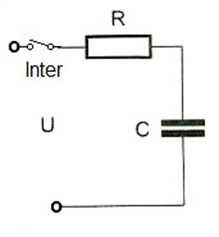
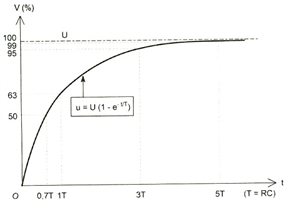
- Charge du condensateur au travers d'une résistance : Figure 1 

- C'est l'utilisation la plus courante des condensateurs. Lorsque l'on regarde la figure2, on constate que la charge du condensateur n'est pas linéaire mais suit une courbe exponentielle. Cette courbe suit la relation u = U ( 1 - e - t/RC ) .
 On sait maintenant (voir la page des condensateurs) que τ=RC avec R en Ohms et C en Farad (cette dernière formule est appelé constante de temps, la formule précédente devient donc. u = U ( 1 - e - t/τ ). Avec u = tension de la courbe à un instant donné. U = tension de la source, R = résistance série et C = capacité. e étant la base des log népériens, soit environ 2,72 
- Pourquoi cela suit-il une courbe exponentielle, et bien à l'instant T1 l'interrupteur est ouvert, le condensateur à un potentiel de 0 volt à ses bornes. Fermons l'interrupteur, à ce moment le condensateur commence sa charge de 0 volt à la tension U, la résistance elle à une différence de potentiel égale à U. L'intensité dans la résistance (I=R/U) est plus grande en début de charge qu'a la fin,elle n'est pas constante. 
 
- Courbe universelle décharge et décharge d'un condensateur dans une résistance: Figure 3

- Sur l'ordonnée U en %, et sur l'abscisse la valeur de τ. (secondes). On remarque que pour la valeur de 5 τ la charge du condensateur est pour ainsi dire complète (99%) et que pour 1 τ le condensateur est chargé à 63%. Cette courbe universelle (en bleue pour la charge et en noir pour la décharge) est valable quelque soit la valeur du condensateur, de la résistance, ou de la tension d’alimentation utilisée. Elle évite donc bien d'équations à résoudre, ce qui est le but ici. La décharge d'un condensateur suit une même courbe exponentielle, mais inverse.
 Ainsi a 1 τ le condensateur est déchargé à 37%. (100%-63% = 37%). 
Figure 1
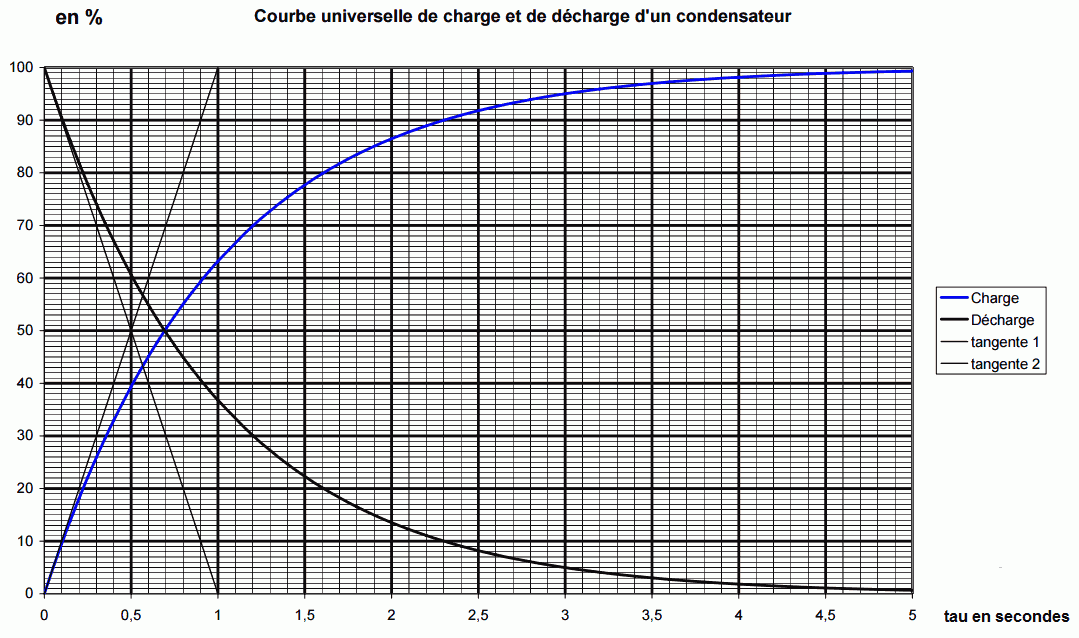
- Exemple d'utilisation de l'abaque avec U = 10V ; R = 10 k ; C = 1000 µF 
- Le condensateur C, étant au départ déchargé, est chargé suivant le montage de la figure 1. 
Calcul de τ, τ = RC donc τ =10 s. (ainsi sur l'abaque 1τ =10 s, 2τ =20 s...5τ =50 s) 
 
1- Quelle est la valeur de la tension aux bornes du condensateur au bout d'un temps de T = 7 secondes. 
Le temps de charge étant de T=7 s et τ =10 secondes, T/τ = 0,7 On repporte sur l’abscisse la valeur de 0,7 et au point de jonction de la courbe de charge (bleue), on lit sur l'ordonnée la valeur de 50% ce qui correspond à 50% de U, soit 5 V. 
 
2- Combien de temps faut-t'il pour que le condensateur atteingne 8 V, la charge de celui-ci commençant à 0 V. 
8 V représente 80% de U (10V). Calcul% = (8*100)/10= 80. La ligne de jonction de 80% sur la courbe de charge correspond à 1,6 τ. Soit 10s (secondes) * 1,6= 16 secondes. 

[1] Le coulomb permet de mesurer la quantité d'électricité qui passe dans un conducteur en de 1 seconde avec une intensité de 1 ampère. Les charges électriques déplacées par les électrons est appelée quantité d'électricité. Elle est notée Q et se mesure en Coulomb (C). 
Recherche sur le site
Recherche sur le web, axée sur l'électronique

L'ensemble du contenu de ce site (y compris les images, les photos, les fichiers et les documents téléchargeables), est protégé par les droits d'auteur et la propriété intellectuelle.